Let ![]() denote the risk-sensitive discounted cost function defined by
denote the risk-sensitive discounted cost function defined by
![\begin{displaymath}J^{\varepsilon,\sqrt{\varepsilon}}(u(\cdot))=\sqrt{\varepsi......\int_0^\infty e^{-\rho t} [h(x(t))+c(u(t))]dt\right\}\right].\end{displaymath}](img1094.gif)
The problem is to find an admissible control ![]() that minimizes
that minimizes ![]() .
.
We now specify the production constraints. For each ![]() ,
let
,
let
With this definition, the production constraint at time t is ![]()
We assume the demand rate z(t) to be a bounded process
independent of ![]() .
.
We say that a control ![]() is admissible if u(t) is a
is admissible if u(t) is a ![]() -adapted
measurable process and
-adapted
measurable process and ![]() for all
for all ![]() .
Then our control problem can be written as follows:
.
Then our control problem can be written as follows:
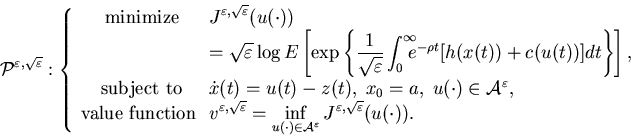
Let ![]() .
We consider the following control space:
.
We consider the following control space:
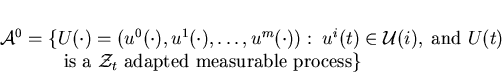
and two control problems ![]() and
and ![]() defined as follows:
defined as follows:
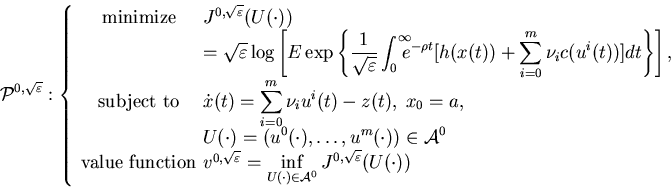
and
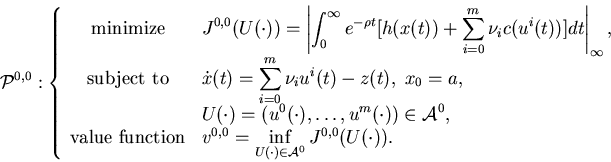
It can be seen below that when ![]() is small,
is small, ![]() can be approximated by
can be approximated by ![]() and
and ![]() can be approximated further by
can be approximated further by![]() .
Therefore,
.
Therefore, ![]() can be approximated by
can be approximated by ![]() .
Then, a near optimal control for
.
Then, a near optimal control for ![]() will be used to construct controls for
will be used to construct controls for ![]() that are nearly optimal.
that are nearly optimal.
Theorem 6.1 There exist
constants ![]() and C such that, for
and C such that, for ![]() ,
,
We show that ![]() can be approximated by
can be approximated by ![]() and the value function of
and the value function of ![]() is a viscosity solution to the Isaacs equation of a zero-sum, two-player
differential game. To simplify the notation, we take
is a viscosity solution to the Isaacs equation of a zero-sum, two-player
differential game. To simplify the notation, we take ![]() and consider the following control problem
and consider the following control problem ![]() .
.
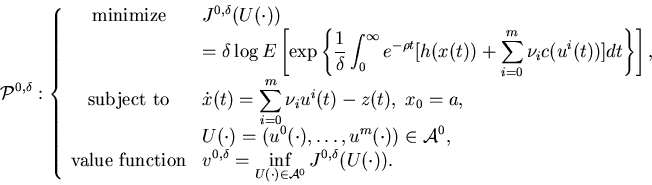
Theorem 6.2![]() is
a monotone increasing function of
is
a monotone increasing function of ![]() and
and
For each ![]() .
.
We write v0,0(x) as the value function of![]() with the initial value x0=x. Note that
with the initial value x0=x. Note that ![]() for any random variable
for any random variable ![]() .
Let
.
Let ![]() such that
such that ![]() and let
and let ![]() denote a compact subset of Rn. We consider functions
denote a compact subset of Rn. We consider functions ![]() (
(![]() )
that are right-continuous and have left-hand limits. Let
)
that are right-continuous and have left-hand limits. Let ![]() denote the metric space of such functions that is equipped with the Skorohod
topology
denote the metric space of such functions that is equipped with the Skorohod
topology ![]() .
.
We assume ![]() a.s. and for each
a.s. and for each ![]() and any
and any ![]() ,
, ![]() .
.
Theorem 6.3 v0,0(x) is the only viscosity solution to the following Isaacs equation:
![\begin{displaymath}\begin{array}{rl}\rho v^{0,0}(x)=&\displaystyle \min_{U\i......,0}_x(x)+h(x)+\sum_{i=0}^m \nu_ic(u^i)\biggr].\end{array}\end{displaymath}](img1132.gif)
Theorem 6.4 The following
assertions hold:
(i)
(ii) Let![]() denote
a stochastic open loop
denote
a stochastic open loop ![]() -optimal
control for
-optimal
control for ![]() ,
i.e.,
,
i.e.,
Let 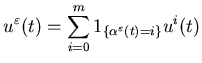 ,
where 1A denotes the indicator of a set A. Then,
,
where 1A denotes the indicator of a set A. Then, ![]() and
and
(iii) Let![]() denote
a feedback
denote
a feedback ![]() -optimal
control for
-optimal
control for ![]() ,
i.e.,
,
i.e.,![]() Let
Let
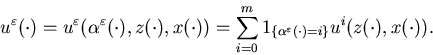
Assume that U(z,x) is locally Lipschitz in x, i.e., for some k>0,
Then, ![]() and
and