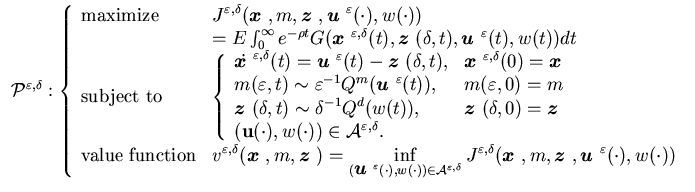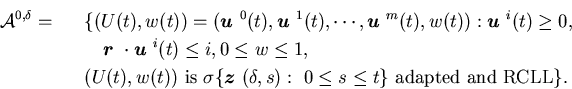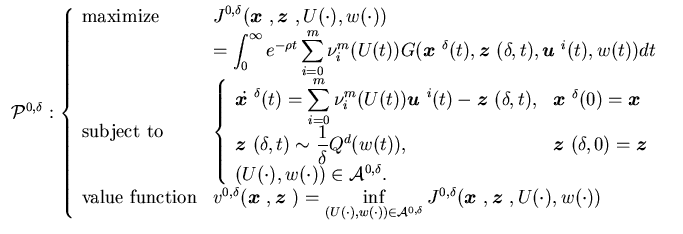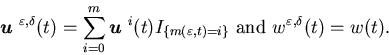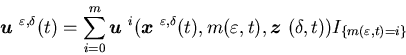

Next:3.6
Computational resultsUp:3.
Hierarchical Controls under DiscountedPrevious:3.4
Hierarchical controls for production-investment
3.5 Hierarchical controls for other multilevel models
Sethi and Zhang (1992b), and Sethi
and Zhang (1995a) extend the model in Section 3.1
to incorporate promotional or advertising decisions that influence the
product demands. Zhou and Sethi (1994)
demonstrate
how workforce and production decisions can be decomposed hierarchically
in a stochastic version of the classical HMMS model Holt,
Modigliani, Muth, and Simon (1960). Manufacturing systems involving
preventive maintenance are studied by Boukas and
Haurie (1990), Boukas (1991), Boukas,
Zhang, and Zhou (1993), and Boukas, Zhu
and Zhang (1994). The maintenance activity involves lubrication, routine
adjustment, etc., which reduce the machine failure rates. The objective
in these systems is to choose the rate of maintenance and the rate of production
in order to minimize the total discounted cost of surplus, production,
and maintenance.
In this section, we shall only discuss the model developed in Sethi
and Zhang (1995a), we consider the case when both capacity and demand
are finite state Markov processes constructed from generators that depend
on the production and promotional decisions, respectively. In order to
specify their marketing-production problem, let 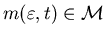 as in Section 3.1 and
as in Section 3.1 and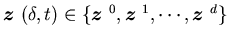 ,
for a given
,
for a given 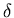 ,
denote the capacity process and the demand process, respectively.
,
denote the capacity process and the demand process, respectively.
Definition 3.7 We say that a
control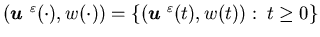 is admissible, if
is admissible, if
-
(i)
-
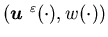 is right-continuous having left-hand limit (RCLL);
is right-continuous having left-hand limit (RCLL);
-
(ii)
-
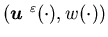 is
is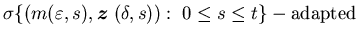 ,
and satisfies
,
and satisfies 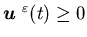 ,
,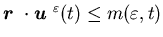 and
and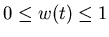 for all
for all 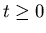 .
.
We use 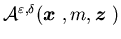 to denote the set of all admissible controls. Then our control problem
can be written as follows:
to denote the set of all admissible controls. Then our control problem
can be written as follows:
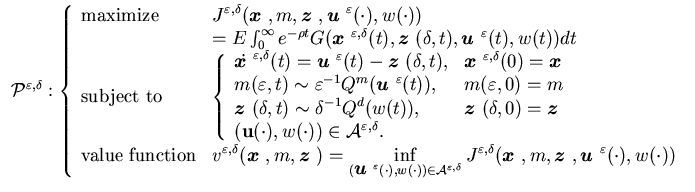 |
|
|
(3.31) |
where by 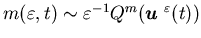 ,
we mean that the Markov process
,
we mean that the Markov process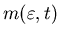 has the generator
has the generator 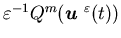 .
.
We use 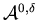 to denote the admissible control space
to denote the admissible control space
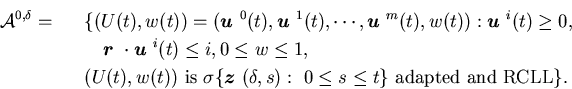
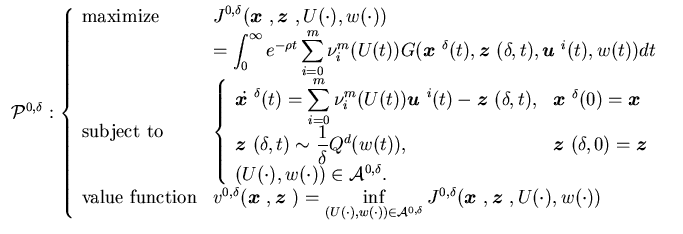
|
|
|
(3.32) |
Let 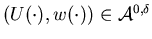 denote an optimal open-loop control. We construct
denote an optimal open-loop control. We construct
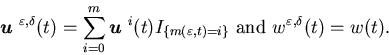 Then
Then 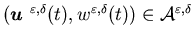 ,
and it is asymptotically optimal, i.e.,
,
and it is asymptotically optimal, i.e.,
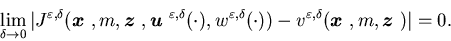 Similarly, let
Similarly, let 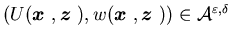 denote an optimal feedback control for
denote an optimal feedback control for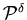 .
Suppose that
.
Suppose that 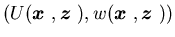 is locally Lipschitz for each
is locally Lipschitz for each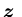 .
Let
.
Let
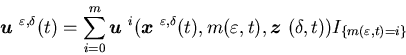 and
and
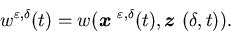 Then the feedback control
Then the feedback control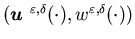 is asymptotically optimal for
is asymptotically optimal for 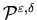 ,
i.e.,
,
i.e.,
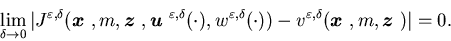 We have described only the hierarchy that arises from a large
We have described only the hierarchy that arises from a large and a small
and a small  .
In this case, promotional decisions are obtained under the assumption that
the available production capacity is equal to the average capacity. Subsequently,
production decisions taking into account the stochastic nature of the capacity
can be constructed. Other possible hierarchies result when both
.
In this case, promotional decisions are obtained under the assumption that
the available production capacity is equal to the average capacity. Subsequently,
production decisions taking into account the stochastic nature of the capacity
can be constructed. Other possible hierarchies result when both 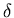 and
and 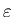 are small or when
are small or when 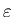 is large and
is large and 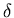 is small. The reader is referred to Sethi and
Zhang (1995a) for details on these.
is small. The reader is referred to Sethi and
Zhang (1995a) for details on these.


Next:3.6
Computational resultsUp:3.
Hierarchical Controls under DiscountedPrevious:3.4
Hierarchical controls for production-investment
![]() as in Section 3.1 and
as in Section 3.1 and![]() ,
for a given
,
for a given ![]() ,
denote the capacity process and the demand process, respectively.
,
denote the capacity process and the demand process, respectively.
![]() is admissible, if
is admissible, if