Next:4. Optimal Control with the Up:3. Hierarchical Controls under Discounted Previous:3.5 Hierarchical controls for other
![]()
![]()
![]()
Next:4.
Optimal Control with the Up:3.
Hierarchical Controls under Discounted Previous:3.5
Hierarchical controls for other
One of the main weaknesses of the early version of Hiercsim for the purpose of this review was its inability to deal with internal storage, see also Violette and Gershwin (1991). Bai (1991) and Bai and Gershwin (1990) developed a hierarchical scheme based on partitioning machines in the original flowshop or jobshop into a number of virtual machines each devoted to single part type production. Violette (1993) developed a modified version of Hiercsim to incorporate the method of Bai and Gershwin (1990). Violette and Gershwin (1991) perform a simulation study indicating that the modified method is efficient and effective. We shall not review it further, since the procedure based on partitioning of machines is unlikely to be asymptotically optimal.
As we indicated in Section 3.2, Sethi,
and Zhou (1996b) have constructed asymptotically optimal hierarchical
controls ![]() ,
given in (3.16) with switching manifolds
depicted in Figure 3.1, for the two-machine flowshop defined by (3.8)
and (3.14). Samaratunga,
Sethi, and Zhou (1997) have compared the performance of these hierarchical
controls (HC) to that of optimal control (OC) and of two other existing
heuristic methods known as Kanban Control (KC) and Two-Boundary Control
(TBC). Like HC, KC is a two parameter policy defined as follows:
,
given in (3.16) with switching manifolds
depicted in Figure 3.1, for the two-machine flowshop defined by (3.8)
and (3.14). Samaratunga,
Sethi, and Zhou (1997) have compared the performance of these hierarchical
controls (HC) to that of optimal control (OC) and of two other existing
heuristic methods known as Kanban Control (KC) and Two-Boundary Control
(TBC). Like HC, KC is a two parameter policy defined as follows:
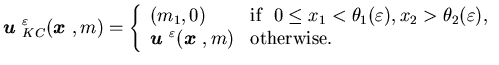 |
(3.33) |
In what follows, we provide the computational results obtained in [Samaratunga, Sethi, and Zhou (1997)] for the problem (3.8) and (3.14) with
In Table 3.1, different initial states are selected and the best parameter values are computed for these different initial states for HC and KC; note from Remark 3.6 that in general there are no parameter values that are best for all possible initial states. In the last row, the initial state (2.70, 1.59) is such that the best hedging point for HC and KC are (2.70,1.59). Table 3.2 uses the parameter values obtained in Table 3.1 in the row with the initial state (0,0).
Samaratunga, Sethi, and Zhou (1997) analyze these computational results and provide the following comparison of OC and KC.
|
(X1,X2) |
|
||||
|
|
|
|
|||
|
|
Parameters | Cost | Parameters | ||
| (0,50) | 771.45 | (0.00,1.00) | 771.45 | (0.00,1.00) | 770.31 |
| (0,20) | 252.72 | (3.51,1.52) | 253.53 | (0.00,3.00) | 231.38 |
| (0,10) | 150.77 | (3.00,2.00) | 151.85 | (0.00,3.22) | 101.13 |
| (0,5) | 132.08 | (2.34,2.06) | 132.16 | (2.29,1.81) | 69.11 |
| (0,0) | 132.76 | (2.75,1.58) | 132.76 | (2.75,1.58) | 66.56 |
| (0,-5) | 288.17 | (3.75,1.50) | 288.17 | (3.75,1.50) | 239.45 |
| (0,-10) | 617.27 | (4.25,1.25) | 617.27 | (4.25,1.25) | 590.67 |
| (0,-20) | 1469.54 | (1.00,0.00) | 1469.54 | (1.00,0.00) | 1466.54 |
| (20,20) | 414.78 | (1.00,1.00) | 414.98 | (0.50,2.50) | 406.96 |
| (10,10) | 194.74 | (2.33,2.36) | 194.74 | (2.33,2.35) | 165.71 |
| (5,5) | 136.80 | (2.79,1.64) | 136.8 | (2.49,1.79) | 84.49 |
| (5,5) | 267.87 | (4.98,1.22) | 267.87 | (4.98,1.22) | 214.46 |
| (10,-10) | 586.04 | (6.41,0.72) | 586.04 | (6.41,0.72) | 539.86 |
| (20,-20) | 1420.34 | (1.00,0.00) | 1420.34 | (1.00,0.00) | 1411.65 |
| (2.70,1.59) | 129.46 | (2.70,1.59) | 129.46 | (2.70,1.59) | 65.39 |
Note: Simulation Relative Error <= 2%, Confidence Level = 95%.
Comparison is carried out for the same machine failure breakdown sample
paths for all policies. OC is obtained from a Markov decision process formulation
of the problem.
|
(X1,X2) |
|
||
| HC Cost | KC Cost | OC Cost | |
| (0,50) | 771.45 | 794.96 | 770.31 |
| (0,20) | 252.78 | 269.12 | 231.38 |
| (0,10) | 150.94 | 156.79 | 101.13 |
| (0,5) | 132.31 | 132.31 | 69.11 |
| (0,0) | 132.76 | 132.76 | 66.56 |
| (0,-5) | 288.34 | 288.34 | 239.45 |
| (0,-10) | 617.85 | 617.85 | 590.67 |
| (0,-20) | 1471.18 | 1471.18 | 1466.54 |
| (20,20) | 415.03 | 415.03 | 406.96 |
| (10,10) | 194.83 | 194.83 | 165.71 |
| (5,5) | 136.82 | 136.82 | 84.49 |
| (5,-5) | 270.75 | 270.75 | 214.46 |
| (10,-10) | 583.85 | 583.85 | 539.86 |
| (20,-20) | 1426.58 | 1426.58 | 1411.65 |
Note: Simulation Relative Error <= 2%, Confidence Level = 95%.
Comparison is carried out for the same machine failure breakdown sample
paths. Therefore, the relative comparison is free of statistical uncertainty.
Thresholds values used for HC as well as KC are (2.75,1.58) obtained from
the (0,0) initial inventory row of Table 3.1.
HC vs. OC
In Table 3.1 and 3.2, the cost of HC is quite close to the optimal cost, if the initial state is sufficiently removed from point (0,0). Moreover, the farther the initial (x1,x2) is from point (0,0), the better the approximation HC provides to OC. This is because the hedging points are close to point (0,0), and hierarchical and optimal controls agree at points in the state space that are further from (0,0) or further from hedging points. In these cases, transients contribute a great deal to the total cost and transients of HC and OC agree in regions far away from (0,0).
HC vs. KC
Let us now compare HC and KC in detail. Of course, if the initial state
is in a shortage situation (![]() ),
then HC and KC must have identical costs. This can be easily seen in Table
3.1 or Table 3.2 when initial (x1,
x2)
= (0, -5), (0, -10), (0, -20), (5, -5), (10, -10) and (20, -20). On the
other hand, if the initial surplus is positive, cost of HC is either the
same as or slightly smaller than the cost of KC, as should be expected.
This is because, KC being a threshold-type policy, the system approaches
),
then HC and KC must have identical costs. This can be easily seen in Table
3.1 or Table 3.2 when initial (x1,
x2)
= (0, -5), (0, -10), (0, -20), (5, -5), (10, -10) and (20, -20). On the
other hand, if the initial surplus is positive, cost of HC is either the
same as or slightly smaller than the cost of KC, as should be expected.
This is because, KC being a threshold-type policy, the system approaches ![]() even when there is large positive surplus, implying higher inventory costs.
In Table 3.1 and Table
3.2, we can see this in rows with initial (x1, x2)
= (0, 5), (0, 10), (0, 20), and (20, 20). Moreover, by the same argument
the values of
even when there is large positive surplus, implying higher inventory costs.
In Table 3.1 and Table
3.2, we can see this in rows with initial (x1, x2)
= (0, 5), (0, 10), (0, 20), and (20, 20). Moreover, by the same argument
the values of ![]() for KC must not be larger than those for HC in Table
3.1. Indeed, in cases with large positive surplus, the value of
for KC must not be larger than those for HC in Table
3.1. Indeed, in cases with large positive surplus, the value of ![]() for KC must be smaller than that for HC. Furthermore, in these cases with
positive surplus, the cost differences in Table
3.2 must be larger than those in Table 3.1, since
Table
3.2 uses hedging point parameters that are best for initial (x1,x2)
= (0,0). These parameters are the same for HC and KC. Thus, the system
with an initial surplus has higher inventories in the internal buffer with
KC than with HC. Note also that if the surplus is very large, then KC in
order to achieve lower inventory costs sets
for KC must be smaller than that for HC. Furthermore, in these cases with
positive surplus, the cost differences in Table
3.2 must be larger than those in Table 3.1, since
Table
3.2 uses hedging point parameters that are best for initial (x1,x2)
= (0,0). These parameters are the same for HC and KC. Thus, the system
with an initial surplus has higher inventories in the internal buffer with
KC than with HC. Note also that if the surplus is very large, then KC in
order to achieve lower inventory costs sets ![]() = 0, with the consequence that its cost is the same as that for HC. For
example, this happens when the initial (x1,x2)
= (0,50) in Table 3.1. As should be expected,
the difference in cost for initial (x1,x2)
= (0,50) in Table 3.2 is quite large compared
to the corresponding difference in Table 3.1.
= 0, with the consequence that its cost is the same as that for HC. For
example, this happens when the initial (x1,x2)
= (0,50) in Table 3.1. As should be expected,
the difference in cost for initial (x1,x2)
= (0,50) in Table 3.2 is quite large compared
to the corresponding difference in Table 3.1.
![]()
![]()
![]()
Next:4.
Optimal Control with the Up:3.
Hierarchical Controls under Discounted Previous:3.5
Hierarchical controls for other