

Next:3.4
Hierarchical controls for production-investmentUp:3.
Hierarchical Controls under DiscountedPrevious:3.2
Hierarchical controls for flowshops
3.3 Hierarchical controls for jobshops
Sethi, and Zhou (1994) consider hierarchical
production planning in a general manufacturing system given in Section
2.3.
For the jobshop 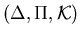 ,
let
,
let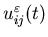 be the control at time t associated with arc (i,j),
be the control at time t associated with arc (i,j), 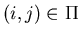 .
Suppose we are given a stochastic process
.
Suppose we are given a stochastic process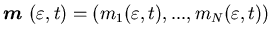 on the standard probability space
on the standard probability space 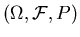 with
with representing the capacity of the nth machine at time t, n=1,...,N,
where
representing the capacity of the nth machine at time t, n=1,...,N,
where 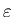 is a small parameter to be precisely specified later. The controls
is a small parameter to be precisely specified later. The controls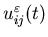 with
with 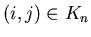 ,
n=1,...,N,
,
n=1,...,N,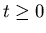 ,
should satisfy the following constraints:
,
should satisfy the following constraints:
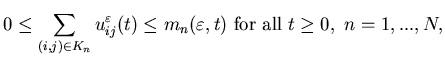
|
|
|
(3.17) |
where we have assumed that the required machine capacity pij
(for unit production rate of type j from part type i) equals
1, for convenience in exposition. The analysis in this paper can be readily
extended to the case when the required machine capacity for the unit production
rate of part j from part i is any given positive constant.
We denote the surplus at time t in buffer i by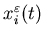 ,
,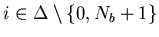 .
Note that if
.
Note that if 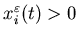 ,
i=1,...,Nb,
we have an inventory in buffer i, and if
,
i=1,...,Nb,
we have an inventory in buffer i, and if 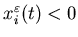 ,
i=m+1,...,Nb,
we have a shortage of finished product i. The dynamics of the system
are therefore
,
i=m+1,...,Nb,
we have a shortage of finished product i. The dynamics of the system
are therefore
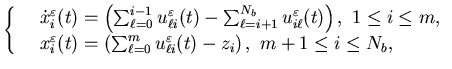
|
|
|
(3.18) |
with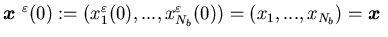 .
.
Let
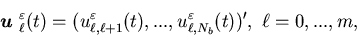
and
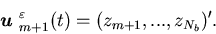
Similar to Section 2.3, we write the relation
(3.18) in the following vector form:
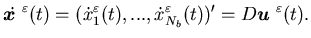
|
|
|
(3.19) |
Definition 3.3 We say that a control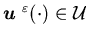 is admissible with respect to the initial state vector
is admissible with respect to the initial state vector 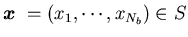 and
and 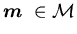 ,
if
,
if
-
(i)
-
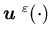 is an
is an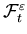 -adapted
measurable process with
-adapted
measurable process with 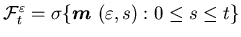 ;
;
-
(ii)
-
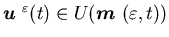 for all
for all 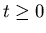 ;
;
-
(iii)
-
the corresponding state process
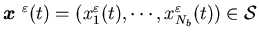 for all
for all 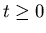 .
.
Remark 3.8 The condition (iii)
is equivalent to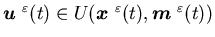 ,
,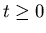 .Let
.Let 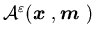 denote the set of all admissible control with respect to
denote the set of all admissible control with respect to 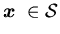 and the machine capacity vector
and the machine capacity vector 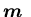 .
The problem is to find an admissible control
.
The problem is to find an admissible control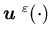 that minimize the cost function
that minimize the cost function
![$\displaystyle J^{\varepsilon}({\mbox{\boldmath$x$ }}, {\mbox{\boldmath$m$ }},{\......oldmath$x$ }}^{\varepsilon}(t))+c( {\mbox{\boldmath$u$ }}^{\varepsilon}(t))]dt,$](img413.gif)
|
|
|
(3.20) |
where 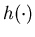 defines the cost of inventory/shortage,
defines the cost of inventory/shortage,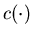 is the production cost,
is the production cost, 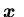 is the initial state, and
is the initial state, and 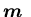 is the initial value of
is the initial value of 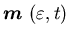 .
.
The value function is then defined as
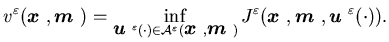
|
|
|
(3.21) |
We impose the following assumptions on the random capacity process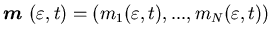 and the cost functions
and the cost functions 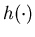 and
and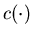 throughout this section.
throughout this section.
Assumption 3.4 Let 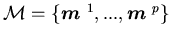 for some given integer
for some given integer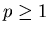 ,
where
,
where 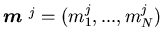 ,
with mjk,
k=1,...,N
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process
,
with mjk,
k=1,...,N
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process 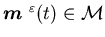 is a finite state Markov chain with the infinitesimal generator
is a finite state Markov chain with the infinitesimal generator 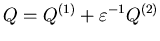 ,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that
,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that 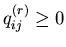 if
if 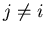 ,
and
,
and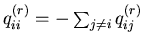 for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies
for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies
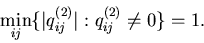 Assumption 3.5 Assume that Q(2)
is weakly irreducible. Let
Assumption 3.5 Assume that Q(2)
is weakly irreducible. Let 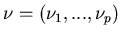 denote the equilibrium distribution of Q(2), that is,
denote the equilibrium distribution of Q(2), that is,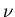 is the only nonnegative solution to the equations
is the only nonnegative solution to the equations
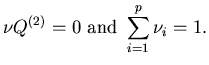
|
|
|
(3.22) |
Assumption 3.6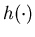 and
and 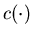 are convex functions. For all
are convex functions. For all 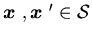 and
and 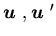 ,
there exist constants C34 and
,
there exist constants C34 and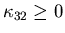 such that
such that
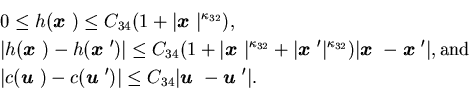
We use 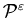 to denote our control problem
to denote our control problem
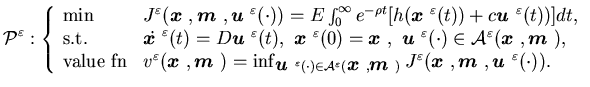
|
|
|
(3.23) |
In order to obtain the limiting problem, we consider the class of deterministic
controls defined below.
Definition 3.4 For 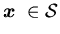 ,
let
,
let 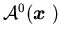 denote the set of the following measurable controls
denote the set of the following measurable controls
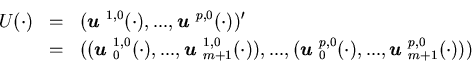 with
with 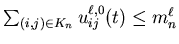 ,
,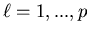 ,
n=1,...,N,
and the corresponding solution
,
n=1,...,N,
and the corresponding solution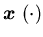 of the system
of the system
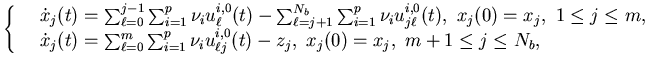 |
|
|
(3.24) |
satisfies 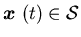 for all
for all 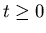 .
.
The object of the limiting problem is to choose a control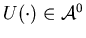 that minimizes
that minimizes
![\begin{eqnarray*}J^0({\mbox{\boldmath$x$ }},U(\cdot))=\int^{\infty}_0 e^{- \rh......1}^p\nu_{\ell}c({\mbox{\boldmath$u$ }}^{\ell,0}(t))\right]dt.\end{eqnarray*}](img431.gif) We write (3.24) in the vector form
We write (3.24) in the vector form
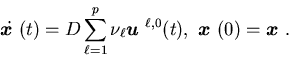
We use 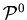 to denote the limiting problem and derive it as follows:
to denote the limiting problem and derive it as follows:
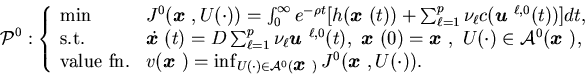
Based on the Lipschitz continuity of the value function given in Section
2.3, Sethi, and
Zhou (1994) prove the following theorem, which says that the problem 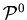 is indeed a limiting problem in the sense that the value function
is indeed a limiting problem in the sense that the value function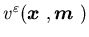 of
of 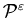 converges to the value function
converges to the value function  of
of 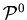 .
Furthermore, the theorem also gives the corresponding convergence rate.
.
Furthermore, the theorem also gives the corresponding convergence rate.
Theorem 3.2 For each 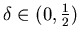 ,
there exists a positive constant C35 such that for all
,
there exists a positive constant C35 such that for all 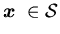 and sufficiently small
and sufficiently small 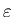 ,
we have
,
we have
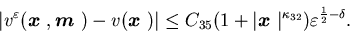
Based on Presman, Sethi, and Suo (1997a),
which is related to the Lipschitz continuity of the value function for
the general jobshop subject to lower and upper bound constraints on work-in-process,
Sethi,
Zhang and Zhang (1999d) also show that Theorem
3.2 is true for a general jobshop system with limited buffers.


Next:3.4
Hierarchical controls for production-investmentUp:3.
Hierarchical Controls under DiscountedPrevious:3.2
Hierarchical controls for flowshops
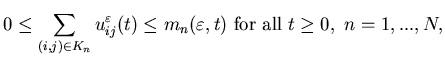
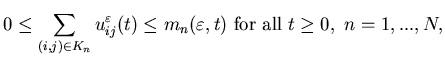
![]() ,
,![]() .
Note that if
.
Note that if ![]() ,
i=1,...,Nb,
we have an inventory in buffer i, and if
,
i=1,...,Nb,
we have an inventory in buffer i, and if ![]() ,
i=m+1,...,Nb,
we have a shortage of finished product i. The dynamics of the system
are therefore
,
i=m+1,...,Nb,
we have a shortage of finished product i. The dynamics of the system
are therefore
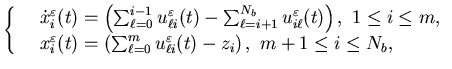
![$\displaystyle J^{\varepsilon}({\mbox{\boldmath$x$ }}, {\mbox{\boldmath$m$ }},{\......oldmath$x$ }}^{\varepsilon}(t))+c( {\mbox{\boldmath$u$ }}^{\varepsilon}(t))]dt,$](img413.gif)
![]() for some given integer
for some given integer![]() ,
where
,
where ![]() ,
with mjk,
k=1,...,N
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process
,
with mjk,
k=1,...,N
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process ![]() is a finite state Markov chain with the infinitesimal generator
is a finite state Markov chain with the infinitesimal generator ![]() ,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that
,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that ![]() if
if ![]() ,
and
,
and![]() for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies
for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies
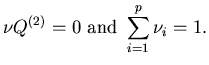
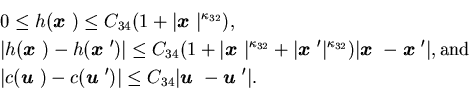
![]() to denote our control problem
to denote our control problem
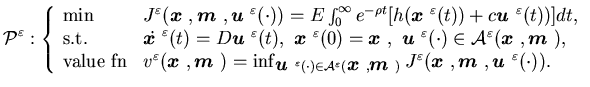
![]() ,
let
,
let ![]() denote the set of the following measurable controls
denote the set of the following measurable controls
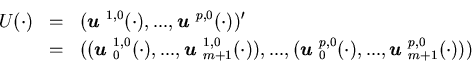
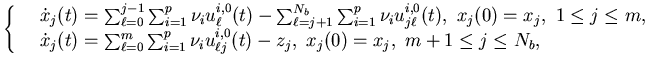
![]() that minimizes
that minimizes
![\begin{eqnarray*}J^0({\mbox{\boldmath$x$ }},U(\cdot))=\int^{\infty}_0 e^{- \rh......1}^p\nu_{\ell}c({\mbox{\boldmath$u$ }}^{\ell,0}(t))\right]dt.\end{eqnarray*}](img431.gif)
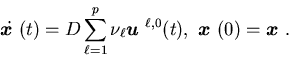
![]() to denote the limiting problem and derive it as follows:
to denote the limiting problem and derive it as follows:
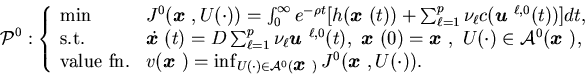
![]() is indeed a limiting problem in the sense that the value function
is indeed a limiting problem in the sense that the value function![]() of
of ![]() converges to the value function
converges to the value function ![]() of
of ![]() .
Furthermore, the theorem also gives the corresponding convergence rate.
.
Furthermore, the theorem also gives the corresponding convergence rate.
![]() ,
there exists a positive constant C35 such that for all
,
there exists a positive constant C35 such that for all ![]() and sufficiently small
and sufficiently small ![]() ,
we have
,
we have