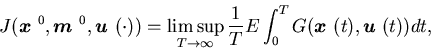 |
(4.17) |
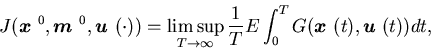 |
(4.17) |
Before beginning the discussion of this problem, we give some requirements
on the cost function and the machine capacity process![]() .
In place of Assumptions 2.4 and 2.5
of Section 2.2, we impose the following assumptions
on the process
.
In place of Assumptions 2.4 and 2.5
of Section 2.2, we impose the following assumptions
on the process![]() throughout this section.
throughout this section.
Assumption 4.4 The Markov process ![]() is strongly irreducible and has the stationary distribution
is strongly irreducible and has the stationary distribution ![]() ,
,![]() .
Let
.
Let ![]() .
Assume that
.
Assume that
Remark 4.6 Assumption 4.4
is not needed in the discounted case. It is clear that this assumption
is necessary for the finiteness of the long-run average cost in the case
when ![]() goes to
goes to ![]() as
as ![]() .As
in Section 2.2, we use
.As
in Section 2.2, we use ![]() to denote the set of all admissible controls with respect to
to denote the set of all admissible controls with respect to ![]() and
and ![]() .
Let
.
Let ![]() denote the minimal expected cost, i.e.,
denote the minimal expected cost, i.e.,
| (4.18) |
Consider now the following equation:
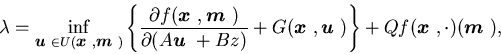 |
(4.19) |
Presman, Sethi, and Zhang (1999a) prove the following verification theorem.
Theorem 4.8 Assume (i) ![]() with
with ![]()
![]() satisfies
(4.19); (ii) there exists a constant
function
satisfies
(4.19); (ii) there exists a constant
function![]() for
which
for
which
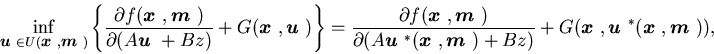 |
(4.20) |
| (4.21) |
| = | ![$\displaystyle \inf_{{\footnotesize\mbox{\boldmath$u$ }}(\cdot )\in {\cal A}({\......ambda \right) dt+f({\mbox{\boldmath$x$ }}(T),{\mbox{\boldmath$m$ }}(T))\right]$](img661.gif) |
||
| = | ![$\displaystyle E\left[ \int_{0}^{T}\left( G({\mbox{\boldmath$x$ }}^{\ast }(t),{......ht) dt+f({\mbox{\boldmath$x$ }}^{\ast }(T),{\mbox{\boldmath$m$ }}(T))\right] .$](img662.gif) |
(4.22) |
The next question is the existence of a solution to (4.19),
that is, is there a pair ![]() that satisfies (4.19)? To get the existence,
we use the vanishing discount approach. Consider the corresponding control
problem with the cost discounted at the rate
that satisfies (4.19)? To get the existence,
we use the vanishing discount approach. Consider the corresponding control
problem with the cost discounted at the rate ![]() .
For
.
For ![]() ,
we define the expected discounted cost as
,
we define the expected discounted cost as
Define the value function of the discounted cost problem as
Just as in Section 4.1, we need a technical lemma that states the finiteness of the rth moment of the time from any given state to any other state.
Lemma 4.2 For any ![]() and
and ![]() ,
there exists a control policy
,
there exists a control policy![]() ,
such
that for any
,
such
that for any![]() ,
,
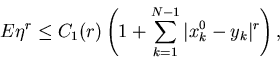 |
(4.23) |
and ![]() is
the surplus process corresponding to the control policy
is
the surplus process corresponding to the control policy ![]() and
the initial condition
and
the initial condition ![]() .
.
Because it is very tricky to construct the desired control, we give
here only the outline of the construction procedure. We begin by modifying
the process ![]() in such a way that the modified average capacity of any machine is larger
than the modified average capacity of the machine that follows it, and
that the modified average capacity of the last machine is larger than z.
Then we alternate between these two policies described below. In the first
policy, the production rate at each machine is the maximum admissible modified
capacity. In the second policy, we stop producing at the first machine
and have the maximum possible production rate at the other machines under
the restriction that the content of each buffer k,
in such a way that the modified average capacity of any machine is larger
than the modified average capacity of the machine that follows it, and
that the modified average capacity of the last machine is larger than z.
Then we alternate between these two policies described below. In the first
policy, the production rate at each machine is the maximum admissible modified
capacity. In the second policy, we stop producing at the first machine
and have the maximum possible production rate at the other machines under
the restriction that the content of each buffer k, ![]() ,
is not less than yk. The first policy is used until such
time when the content of the first buffer exceeds the value y1
and the content of each buffer k,
,
is not less than yk. The first policy is used until such
time when the content of the first buffer exceeds the value y1
and the content of each buffer k,![]() ,
exceeds the value a+yk for some a>0. At
that time we switch to the second policy. We use the second policy until
such time when the content of the last buffer drops to the level yN.
After that we revert to the first policy, and so on. Using this alternating
procedure, it is possible to specify
,
exceeds the value a+yk for some a>0. At
that time we switch to the second policy. We use the second policy until
such time when the content of the last buffer drops to the level yN.
After that we revert to the first policy, and so on. Using this alternating
procedure, it is possible to specify ![]() and provide an estimate for it. For a complete proof, see Presman,
Sethi, and Zhang (1999a).
and provide an estimate for it. For a complete proof, see Presman,
Sethi, and Zhang (1999a).
Based on this lemma, Presman, Sethi, and Zhang (1999a) give the next two theorems which are concerned with the solution of (4.19).
Theorem 4.9 There exists
a sequence ![]() with
with ![]() as
as![]() such that for
such that for ![]() :
:
![\begin{eqnarray*}&&\lim_{k\rightarrow \infty }\rho _{k}V^{\rho _{k}}({\mbox{\b......m$ }}^{0})]=W({\mbox{\boldmath$x$ }},{\mbox{\boldmath$m$ }}),\end{eqnarray*}](img679.gif)
Let ![]() be the derivative of
be the derivative of![]() at the point
at the point ![]() where the derivative exists.
where the derivative exists.
Theorem 4.10 In our problem,
(i) ![]() does not depend on
does not depend on ![]() .
(ii) The pair
.
(ii) The pair![]() defined
in Theorem 4.9 satisfies (4.19)
on
So, where So is the interior of the setS. (iii)
If there exists an open subset
defined
in Theorem 4.9 satisfies (4.19)
on
So, where So is the interior of the setS. (iii)
If there exists an open subset ![]() of S such that
of S such that ![]() ,
where
,
where ![]() is the boundary of
is the boundary of ![]() ,
and
,
and![]() is uniformly equi-Lipschitzian on
is uniformly equi-Lipschitzian on ![]() ,
then the pair
,
then the pair![]() defined
in Theorem 4.9 is a solution to
(4.19).
defined
in Theorem 4.9 is a solution to
(4.19).
Remark 4.7 Note that the statement (i) of Theorem 4.10 follows from Theorem 4.9. The statement (ii) of Theorem 4.10 follows from Theorem 4.9 and a simple limiting procedure.