|
|
(2.5) |
|
|
(2.5) |
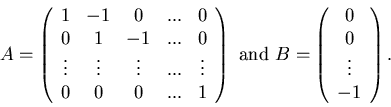
|
|
(2.6) |
| = | |||
| (2.7) |
Definition 2.6 We say that a control ![]() is
admissible with respect to the initial value
is
admissible with respect to the initial value ![]() and
and![]() if
if
Definition 2.7 A function ![]() is call
an admissible feedback control, or simply feedback control,
if
is call
an admissible feedback control, or simply feedback control,
if
has a unique solution with ![]() and
and![]() ;
;
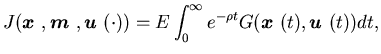 |
(2.8) |
|
|
(2.9) |
We impose the following assumptions on the Markov process![]() and the cost function
and the cost function![]() :
:
Assumption 2.4![]() is a nonnegative jointly convex function that is strictly convex in either
is a nonnegative jointly convex function that is strictly convex in either ![]() or
or ![]() or both. For all
or both. For all ![]() and
and ![]() ,
j=1,...,p,
there exist constants C28 and
,
j=1,...,p,
there exist constants C28 and![]() such that
such that
![\begin{displaymath}Qf(\cdot)({\mbox{\boldmath$m$ }})=\sum_{{\mbox{\boldmath$m$...... }}'}[f({\mbox{\boldmath$m$ }}')-f({\mbox{\boldmath$m$ }})]\end{displaymath}](img133.gif)
The problem of the flowshop with internal buffers and the resulting state constraints is much more complicated. Certain boundary conditions need to be taken into account for the associated HJB equation. Optimal control policy can no longer be described simply in terms of some hedging points.
Lou, Sethi, and Zhang (1994) show that the optimal control policy for a two-machine flowshop with linear costs of production can be given in terms of two switching manifolds. However, the switching manifolds are not easy to obtain. One way to compute them is to approximate them by continuous piecewise-linear functions as done by Van Ryzin, Lou, and Gershwin (1993) in the absence of production costs.
To rigorously deal with the general flowshop problem under consideration, we write the HJB equation in terms of the Directional Derivatives (HJBDD) at inner and boundary points. So, we first give the notion of these derivatives and some related properties of convex functions.
Definition 2.8 A function ![]() ,
,![]() is said to have a directional derivative
is said to have a directional derivative![]() along the direction
along the direction ![]() if the following limit exists, i.e.,
if the following limit exists, i.e.,
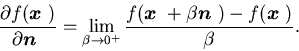
A continuous convex function defined on a convex domain ![]() is differentiable almost everywhere and has a directional derivative both
along any direction at any inner point of
is differentiable almost everywhere and has a directional derivative both
along any direction at any inner point of ![]() and along any admissible direction (i.e., such direction
and along any admissible direction (i.e., such direction ![]() that
that![]() for some
for some ![]() )
at any boundary point of
)
at any boundary point of ![]() .
Note that
.
Note that ![]() is the set of admissible directions at
is the set of admissible directions at![]() .
We can formally write the HJB equation in terms of directional derivative
(HJBDD) for the problem as
.
We can formally write the HJB equation in terms of directional derivative
(HJBDD) for the problem as
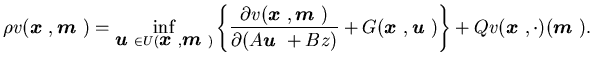 |
(2.10) |
Similar to Theorem 2.1, Presman, Sethi, and Zhang (1995) prove the following theorem.
Theorem 2.6 (i) The value function ![]() is convex and continuous on S and satisfies the condition
is convex and continuous on S and satisfies the condition
|
|
(2.11) |
Furthermore, by introducing an equivalent deterministic problem to the stochastic problem, Presman, Sethi, and Zhang (1995) give the verification theorem along with the existence of the optimal control.
Theorem 2.7 (i) The optimal control![]() exists,
is unique, and can be represented as a feedback control, i.e., there exists
a function
exists,
is unique, and can be represented as a feedback control, i.e., there exists
a function ![]() such
that for any
such
that for any![]() ,
we have
,
we have
(iii) Assume that ![]() is strictly convex in
is strictly convex in![]() for each fixed
for each fixed ![]() .
Let
.
Let ![]() denote
the minimizer function of the right-hand side of (2.10).
Then,
denote
the minimizer function of the right-hand side of (2.10).
Then,
Remark 2.3 Presman, Sethi, and Suo (1997) study the N-machine flowshop with limited buffers. They show that Theorem 2.6 and Theorem 2.7 also hold in the limited buffer case.