

Next:5.3
Hierarchical controls of dynamicUp:5.
Hierarchical Controls under thePrevious:5.1
Hierarchical controls of single
5.2 Hierarchical control of single or parallel machine systems without
deterioration and cancelation rates
Consider a manufacturing system whose system dynamics is given by (5.1)
with ak=0, k=1,...,n,
that is,
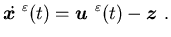
|
|
|
(5.13) |
We assume that the machine capacity process 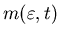 is a finite-state Markov process given in Section 3.1.
Now we define the set of admissible controls as follows:
is a finite-state Markov process given in Section 3.1.
Now we define the set of admissible controls as follows:
Definition 5.3 We say that a
control 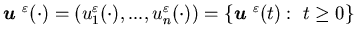 is admissible, if
is admissible, if
-
(i)
-
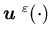 is an
is an 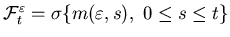 adapted measurable process;
adapted measurable process;
-
(ii)
-
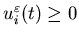 and
and 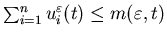 .
.
We use 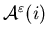 to denote the set of all admissible controls with the initial condition
to denote the set of all admissible controls with the initial condition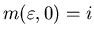 .
.
Definition 5.4 A function 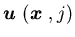 defined on
defined on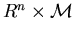 is called an admissible feedback control, or simply a feedback control,
if
is called an admissible feedback control, or simply a feedback control,
if
-
(i)
-
for any given initial surplus
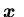 and production capacity i, the equation
and production capacity i, the equation
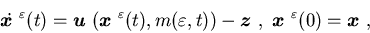
has a unique solution;
-
(ii)
-
the control defined by
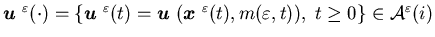 .
.
With a slight abuse of notation, we simply call 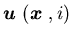 a feedback control when no ambiguity arises. For any
a feedback control when no ambiguity arises. For any 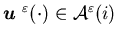 ,
define
,
define
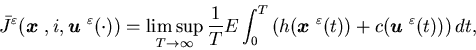 where
where 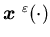 is the surplus process corresponding to the production rate
is the surplus process corresponding to the production rate 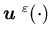 with
with 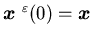 .
Our goal is to choose
.
Our goal is to choose 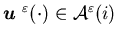 so as to minimize the cost
so as to minimize the cost 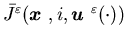 .
We formally summarize the control problem as follows:
.
We formally summarize the control problem as follows:
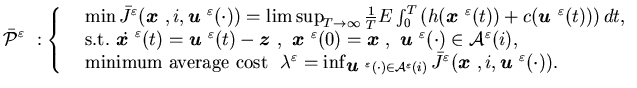
|
|
|
(5.14) |
We make the same assumptions on the surplus cost function 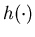 and the production cost function
and the production cost function 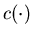 ,
and the Markov chain
,
and the Markov chain 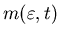 as in Section 5.1. Without a positive inventory
deterioration/cancelation rate for each product type, the system state
as in Section 5.1. Without a positive inventory
deterioration/cancelation rate for each product type, the system state 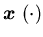 may no longer remain bounded. Thus the approach presented in Section 5.1
cannot be used for the system given by (5.13).
Here we will use the vanishing discount approach to treat the problem.
In order to derive the dynamic programming equation for the average cost
control problem formulated above and carry out an asymptotic analysis of
the minimum long-run average expected cost for (5.14),
we introduce a related control problem with the cost discounted at a rate
may no longer remain bounded. Thus the approach presented in Section 5.1
cannot be used for the system given by (5.13).
Here we will use the vanishing discount approach to treat the problem.
In order to derive the dynamic programming equation for the average cost
control problem formulated above and carry out an asymptotic analysis of
the minimum long-run average expected cost for (5.14),
we introduce a related control problem with the cost discounted at a rate 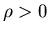 .
For
.
For 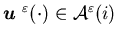 ,
let
,
let 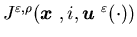 denote the cost function, i.e.,
denote the cost function, i.e.,
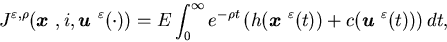
where 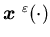 satisfies (5.13), i.e., the surplus process
corresponding to the production rate
satisfies (5.13), i.e., the surplus process
corresponding to the production rate 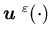 .
Then, our related control problem can be written as (3.3)
in Section 3.1.
.
Then, our related control problem can be written as (3.3)
in Section 3.1.
In order to study the long-run average cost control problem by using
the vanishing discount approach, we must first obtain some estimates for
the value function 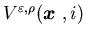 (
(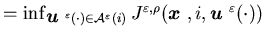 ).
Sethi
and Zhang (1998) prove the following result.
).
Sethi
and Zhang (1998) prove the following result.
Theorem 5.5 There exist
constants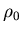 and
and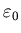 such
that
such
that
-
(i)
-
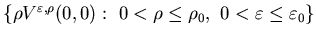 is
bounded;
is
bounded;
-
(ii)
-
For
![$\varepsilon \in (0,\varepsilon_0]$](img825.gif) and
and![$\rho \in (0, \rho_0]$](img826.gif) ,
the
function
,
the
function
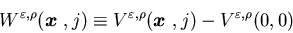
is convex in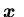 ;
;
-
(iii)
-
For
![$\varepsilon \in (0,\varepsilon_0]$](img825.gif) and
and![$\rho \in (0, \rho_0]$](img826.gif) ,
,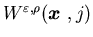 is
locally Lipschitz continuous in x, i.e., there exists a constant
C independent of
is
locally Lipschitz continuous in x, i.e., there exists a constant
C independent of 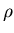 and
and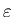 ,
such
that
,
such
that
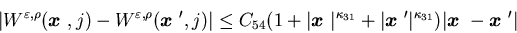
for 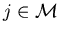 and
all
and
all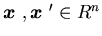 ,
where
,
where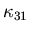 is
given in Assumption 3.2.
is
given in Assumption 3.2.
Corresponding to the dynamic programming equation (3.4)
associated with the discounted cost case, we can formally write the dynamic
programming equation associated with the long-run average cost case as
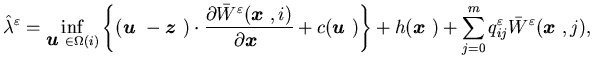 |
|
|
(5.15) |
for any 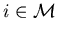 and
and 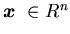 ,
where
,
where 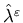 is a constant and
is a constant and 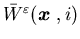 is a real-valued function on
is a real-valued function on 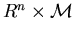 .
.
Lemma 5.1 The dynamic programming
equation (5.15) has a unique solution
in the following sense: If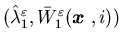 and
and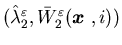 are
viscosity solutions to (5.15), then
are
viscosity solutions to (5.15), then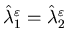 .
.
For the proof, see Theorem G.1 in Sethi and
Zhang (1994a).
Remark 5.3 While the proof of
Theorem G.1 in Sethi and Zhang (1994a) works
for the uniqueness of 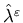 ,
it cannot be adapted to prove whether
,
it cannot be adapted to prove whether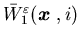 and
and 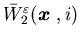 are equal. Clearly, if
are equal. Clearly, if 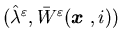 is a viscosity solution to (5.15), then
for any constant
C,
is a viscosity solution to (5.15), then
for any constant
C, 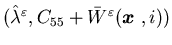 is also a viscosity solution to (5.15).
However, we do not need
is also a viscosity solution to (5.15).
However, we do not need 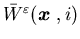 to be unique for the purpose of this paper.According to (i) and (iii) of
Theorem 5.5, for a fixed
to be unique for the purpose of this paper.According to (i) and (iii) of
Theorem 5.5, for a fixed![$\varepsilon \in (0, \epsilon_0]$](img842.gif) and any subsequence of
and any subsequence of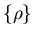 ,
there is a further subsequence denoted by
,
there is a further subsequence denoted by 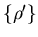 ,
such that
,
such that
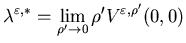
|
|
|
(5.16) |
and
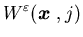 |
= |
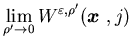 |
(5.17) |
for all 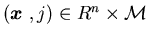 .
Furthermore, we have the following lemma proved in Sethi
and Zhang (1998).
.
Furthermore, we have the following lemma proved in Sethi
and Zhang (1998).
Lemma 5.2 There exists a
constant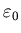 such
that for
such
that for![$\varepsilon \in (0,\varepsilon_0]$](img825.gif)
-
(i)
-
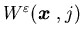 given
in (5.17) is convex and is locally
Lipschitz continuous in
given
in (5.17) is convex and is locally
Lipschitz continuous in 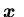 ,
i.e., there is constant C such that
,
i.e., there is constant C such that
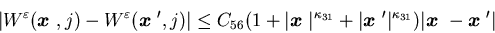
for all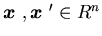 and
and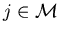 ;
;
-
(ii)
-
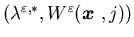 is
a viscosity solution to the dynamic programming equation (5.15);
is
a viscosity solution to the dynamic programming equation (5.15);
-
(iii)
-
there exists a constant C such that for all
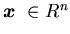 and
and 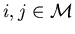 ,
,
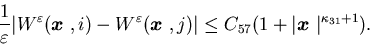
From (ii) of Lemma 5.2, for each subsequence
of 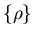 ,
denoted by
,
denoted by 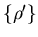 ,
the limit of
,
the limit of 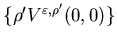 with some function
with some function 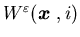 is a viscosity solution to the dynamic programming equation (5.15).
With the help of Lemma 5.1, we get that
is a viscosity solution to the dynamic programming equation (5.15).
With the help of Lemma 5.1, we get that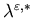 ,
the limit of
,
the limit of 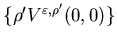 does not depend on the choice of the subsequence
does not depend on the choice of the subsequence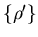 .
Thus, we have the following lemma.
.
Thus, we have the following lemma.
Lemma 5.3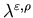 converges
to
converges
to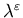 ,
as
,
as 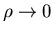 .
.
Multiplying both sides of (5.15) at
i by 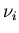 ,
i=0,1,...,p
defined in Assumption 2.3 and summing
over i, we have
,
i=0,1,...,p
defined in Assumption 2.3 and summing
over i, we have
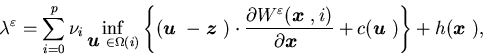
keeping in mind that 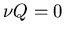 .
Then we let
.
Then we let 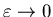 to obtain
to obtain
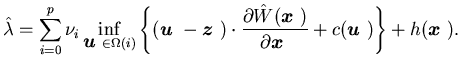
|
|
|
(5.18) |
This procedure will be justified in the next theorem. Note that
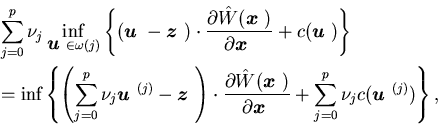 where
where 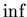 is taken by
is taken by 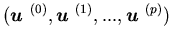 in
in 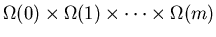 .
Thus, (5.18) is also equivalent to
.
Thus, (5.18) is also equivalent to
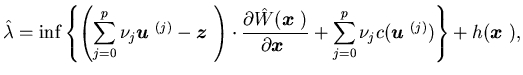
|
|
|
(5.19) |
which is the dynamic programming equation for the following deterministic
problem:
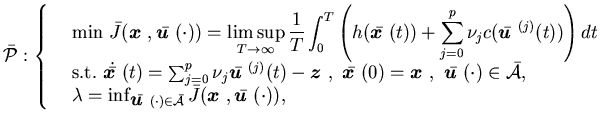
|
|
|
(5.20) |
where
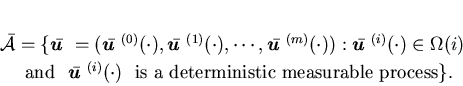 With the help of (i) of Theorem 5.5,
(i) of Lemma 5.2 and Lemma
5.3,
Sethi
and Zhang (1998) derive the convergence of the minimum average expected
cost
With the help of (i) of Theorem 5.5,
(i) of Lemma 5.2 and Lemma
5.3,
Sethi
and Zhang (1998) derive the convergence of the minimum average expected
cost 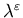 as
as 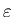 goes to zero.
goes to zero.
Theorem 5.6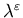 ,
the
minimum average cost of the problem
,
the
minimum average cost of the problem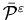 defined
in (5.14), converges to
defined
in (5.14), converges to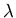 ,
the
minimum average cost of the limiting control problem
,
the
minimum average cost of the limiting control problem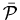 defined
in (5.20), i.e.,
defined
in (5.20), i.e.,
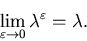


Next:5.3
Hierarchical controls of dynamicUp:5.
Hierarchical Controls under thePrevious:5.1
Hierarchical controls of single
![]() is admissible, if
is admissible, if
![]() defined on
defined on![]() is called an admissible feedback control, or simply a feedback control,
if
is called an admissible feedback control, or simply a feedback control,
if
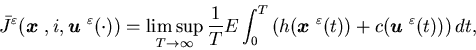
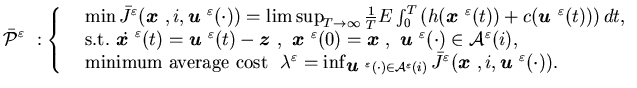
![]() satisfies (5.13), i.e., the surplus process
corresponding to the production rate
satisfies (5.13), i.e., the surplus process
corresponding to the production rate ![]() .
Then, our related control problem can be written as (3.3)
in Section 3.1.
.
Then, our related control problem can be written as (3.3)
in Section 3.1.
![]() (
(![]() ).
Sethi
and Zhang (1998) prove the following result.
).
Sethi
and Zhang (1998) prove the following result.
![]() and
and![]() such
that
such
that
![]() ;
;
![]() and
all
and
all![]() ,
where
,
where![]() is
given in Assumption 3.2.
is
given in Assumption 3.2.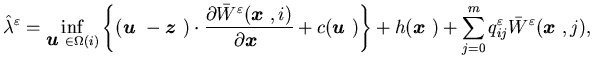
![]() and
and![]() are
viscosity solutions to (5.15), then
are
viscosity solutions to (5.15), then![]() .
.
![]() ,
it cannot be adapted to prove whether
,
it cannot be adapted to prove whether![]() and
and ![]() are equal. Clearly, if
are equal. Clearly, if ![]() is a viscosity solution to (5.15), then
for any constant
C,
is a viscosity solution to (5.15), then
for any constant
C, ![]() is also a viscosity solution to (5.15).
However, we do not need
is also a viscosity solution to (5.15).
However, we do not need ![]() to be unique for the purpose of this paper.According to (i) and (iii) of
Theorem 5.5, for a fixed
to be unique for the purpose of this paper.According to (i) and (iii) of
Theorem 5.5, for a fixed![]() and any subsequence of
and any subsequence of![]() ,
there is a further subsequence denoted by
,
there is a further subsequence denoted by ![]() ,
such that
,
such that
![]() such
that for
such
that for![]()
![]() and
and![]() ;
;
![]() ,
i=0,1,...,p
defined in Assumption 2.3 and summing
over i, we have
,
i=0,1,...,p
defined in Assumption 2.3 and summing
over i, we have
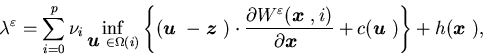
![]() .
Then we let
.
Then we let ![]() to obtain
to obtain
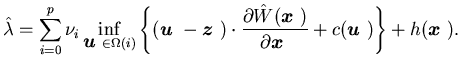
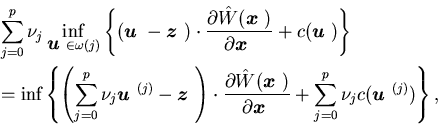
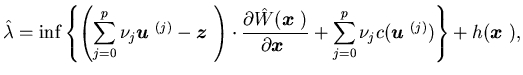
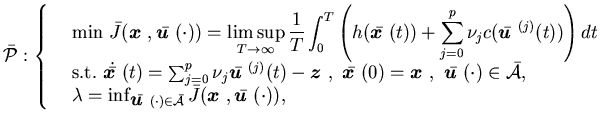
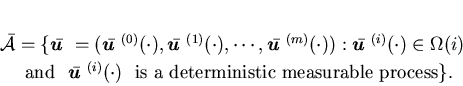
![]() ,
the
minimum average cost of the problem
,
the
minimum average cost of the problem![]() defined
in (5.14), converges to
defined
in (5.14), converges to![]() ,
the
minimum average cost of the limiting control problem
,
the
minimum average cost of the limiting control problem![]() defined
in (5.20), i.e.,
defined
in (5.20), i.e.,