|
|
(5.1) |
|
|
(5.1) |
Let ![]() ,
,![]() ,
denote a Markov process generated by
,
denote a Markov process generated by![]() ,
where
,
where ![]() is a small parameter and
is a small parameter and ![]() ,
,![]() is an (m+1) x (m+1)
matrix such that
is an (m+1) x (m+1)
matrix such that![]() for
for ![]() and
and![]() for
for ![]() .
We let
.
We let ![]() represent the machine capacity state at time t.
represent the machine capacity state at time t.
Definition 5.1 A production
control process![]() is admissible, if
is admissible, if
Definition 5.2 A function ![]() defined on
defined on ![]() is called an admissible feedback control or simply a feedback control,
if
is called an admissible feedback control or simply a feedback control,
if
has a unique solution;
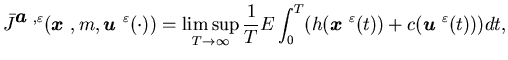 |
(5.2) |
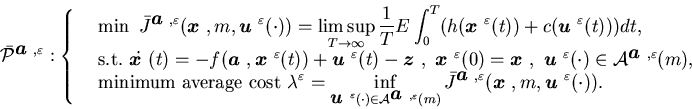
Here we assume that the production cost function ![]() and the surplus cost function
and the surplus cost function ![]() satisfy Assumption 3.1, and the machine
capacity process
satisfy Assumption 3.1, and the machine
capacity process ![]() satisfies Assumptions 3.2 and 3.3.
Furthermore, similar to Assumption
4.3,
we also assume
satisfies Assumptions 3.2 and 3.3.
Furthermore, similar to Assumption
4.3,
we also assume
As in Fleming and Zhang (1998), the positive
attrition rate![]() implies a uniform bound for
implies a uniform bound for ![]() .
In view of the fact that the control
.
In view of the fact that the control ![]() is bounded between 0 and
m, this implies that any solution
is bounded between 0 and
m, this implies that any solution ![]() to (5.1) must satisfy
to (5.1) must satisfy
| = | 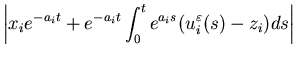 |
||
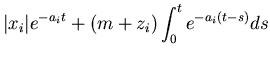 |
|||
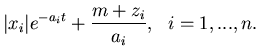 |
(5.3) |
The average cost optimality equation associated with the average-cost
optimal control problem in ![]() ,
as shown in Sethi, Zhang, and Zhang (1997),
takes the form
,
as shown in Sethi, Zhang, and Zhang (1997),
takes the form
| = | 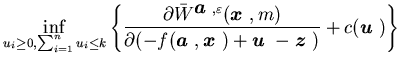 |
||
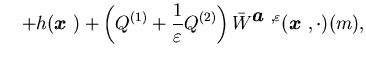 |
(5.4) |
Theorem 5.1 The minimum
average expected cost ![]() of
of ![]() is
bounded in
is
bounded in![]() ,
i.e.,
there exists a constant C>0 such that
,
i.e.,
there exists a constant C>0 such that
In order to construct open-loop and feedback hierarchical controls
for the system, one derives the limiting control problem as![]() .
As in Sethi, Zhang, and Zhou (1994), consider
the enlarged control space
.
As in Sethi, Zhang, and Zhou (1994), consider
the enlarged control space
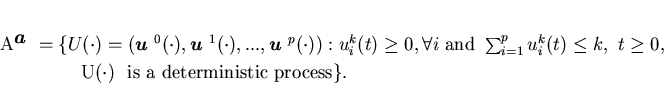
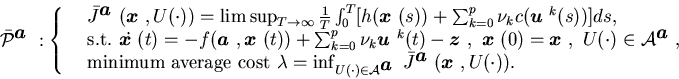
The average-cost optimality equation associated with the limiting control
problem ![]() is
is
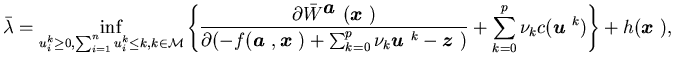 |
(5.5) |
Armed with Theorem 5.1, one can derive
the convergence of the minimum average expected cost ![]() as
as![]() goes to zero, and establish the convergence rate.
goes to zero, and establish the convergence rate.
Theorem 5.2 There exists
a constant C such that for all ![]() ,
,
This implies in particular that ![]() .
.
Here we only outline the major steps in the proof. For the detailed
proof, the reader is referred to Sethi, Zhang,
and Zhang (1997). The first step is to prove ![]() by constructing an admissible control
by constructing an admissible control ![]() of
of ![]() from the optimal control of the limiting problem
from the optimal control of the limiting problem ![]() ,
and by estimating the difference between the state trajectories corresponding
to these two controls. Then one establishes the opposite inequality, namely,
,
and by estimating the difference between the state trajectories corresponding
to these two controls. Then one establishes the opposite inequality, namely,![]() ,
by constructing a control of the limiting problem
,
by constructing a control of the limiting problem![]() from a near-optimal control of
from a near-optimal control of ![]() and then using Assumptions 2.1.
and then using Assumptions 2.1.
The following theorem concerning open-loop controls is proved in Sethi, Zhang, and Zhang (1997).
Theorem 5.3 (Open-loop control)
Let![]() be
an optimal control for
be
an optimal control for![]() ,
and
let
,
and
let
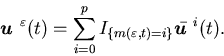
for some positive constant C.
We next consider feedback controls. We begin with an optimal feedback
control for ![]() ,
which with a slight abuse of notation is denoted as
,
which with a slight abuse of notation is denoted as ![]() .
This is obtained by minimizing the right-hand side of (5.5),
i.e.,
.
This is obtained by minimizing the right-hand side of (5.5),
i.e.,
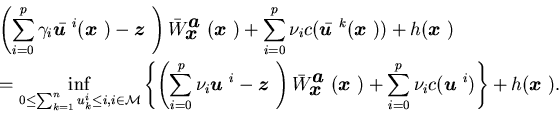
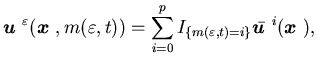 |
(5.6) |
|
|
(5.7) |
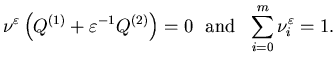 |
(5.8) |
Theorem 5.4 (Feedback control)
Let
n=1. Assume (A.2.1) and (A.9.3) and that the feedback
control of the limiting problem ![]() is
locally Lipschitz in x. Furthermore, suppose that for each
is
locally Lipschitz in x. Furthermore, suppose that for each![]() ,
the
equation
,
the
equation
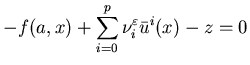 |
(5.9) |
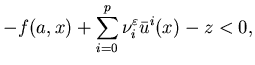 |
(5.10) |
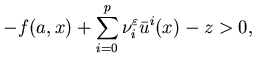 |
(5.11) |
where![]() .
.
Since there are several hypotheses, namely (5.9)-(5.11), in Theorem 5.4, it is important to provide at least an example for which these hypotheses hold. Below we provide such an example and at the same time illustrate the ideas of constructing the asymptotically optimal controls.
Example 5.1. Consider the problem
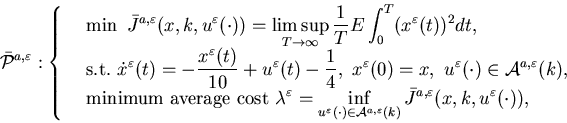
with ![]() and the generator for
and the generator for ![]() to be
to be
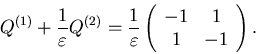
This is clearly a special case of the problem formulated in this section.
In particular, Assumptions 3.3 and 3.4
hold and![]() .
The limiting problem is
.
The limiting problem is
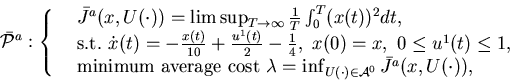
where we use ![]() .
Let us set the function
.
Let us set the function
|
|
(5.12) |
is an asymptotically optimal feedback control for ![]() .
.
Remark 5.1 It is possible to obtain other optimal feedback controls for Example 5.1. It is also possible to provide examples with nonzero production cost, for which Lipschitz feedback controls satisfying (5.9)-(5.11) can be obtained, and their optimality asserted by a verification theorem similar to Theorem 4.3 in Sethi, Suo, Taksar, and Yan (1998).
Remark 5.2 A similar averaging approach is introduced in Altman and Gaitsgory (1993) and Altman and Gaitsgory (1997), Nguyen and Gaitsgory (1997), Shi, Altman and Gaitsgory (1998), Nguyen (1999) and references there in. They consider a class of nonlinear hybrid systems in which the parameters of the dynamics of the system may jump at discrete moments of time, according to a controlled Markov chain with finite states and action spaces. They assume that the unit of the length of intervals between the jumps is small. They prove that the optimal solution of the hybrid systems governed by the controlled Markov chain can be approximated by the solution of a limiting deterministic optimal control problem.