Let us consider a Markov decision process ![]() and a control process
and a control process ![]() such that
such that![]() ,
,![]() ,
where U is a set with finite elements.
,
where U is a set with finite elements.
Let ![]() ,
,![]() ,
denote the generator of
,
denote the generator of ![]() such that
such that
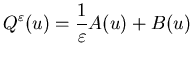 |
(5.51) |
Example 5.2. Let us consider a failure-prone manufacturing system
that consists of a two-machine flowshop. Each of the two machine has two
states up, denoted by 1, and down, denoted by 0. Then, the system has four
states, represented by ![]() .
Let s11=(1,1), s12=(0,1),
s21=(1,0),
and s22=(0,0). We consider u to be the rate of
preventive maintenance, which is used to reduce the failure rate of machines
and to improve the productivity of the system. The objective of the problem
is to choose
u to keep the average machine capacity at a reasonable
level and, in the meantime, to avoid excessive costly preventive maintenance.
.
Let s11=(1,1), s12=(0,1),
s21=(1,0),
and s22=(0,0). We consider u to be the rate of
preventive maintenance, which is used to reduce the failure rate of machines
and to improve the productivity of the system. The objective of the problem
is to choose
u to keep the average machine capacity at a reasonable
level and, in the meantime, to avoid excessive costly preventive maintenance.
We consider the system in which the state of the first machine is changing more rapidly than that of the second one. A typical way of modeling the machine state process is to formulate the process (see Jiang and Sethi (1991), Sethi and Zhang (1994a), and Yin and Zhang (1997) ) as a Markov chain with the following generator:
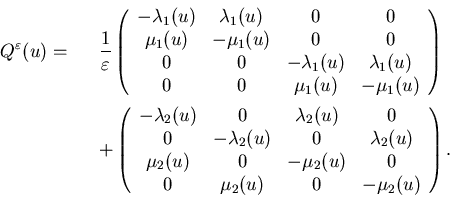
The matrix A(u) dictates the fast transition of the process ![]() within each group
within each group ![]() ,
,![]() and the matrix B(u) together with the average distribution
of the Markov chain generated by Ak(u) dictates
the slow transition of
and the matrix B(u) together with the average distribution
of the Markov chain generated by Ak(u) dictates
the slow transition of![]() between different groups. When
between different groups. When ![]() is small, the process
is small, the process ![]() has a strong interaction within any group
has a strong interaction within any group![]() ,
,![]() and has a weak interaction among these groups.
and has a weak interaction among these groups.
Let u=u(i) denote a function such that ![]() for all
for all ![]() .
We call u an admissible control and use
.
We call u an admissible control and use![]() to denote all such functions. We make the following assumptions:
to denote all such functions. We make the following assumptions:
Assumption 5.6 For each ![]() ,
,![]() is irreducible,
is irreducible, ![]() ,
and for each
,
and for each ![]() ,
,![]() is irreducible, where
is irreducible, where ![]() is defined in (49).
is defined in (49).
Assumption 5.7 U is a finite
set.
We consider the following problem:
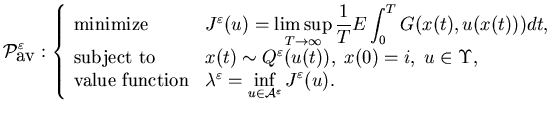 |
(5.52) |
|
|
(5.53) |
To proceed, we define the control set for the limiting problem. Motivated
by Sethi and Zhang (1994a), we consider a
control set in which each control variable corresponds to a state in![]() .
To be more precise, for each
.
To be more precise, for each ![]() ,
let
,
let
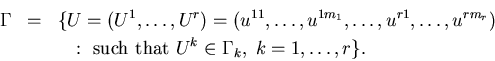
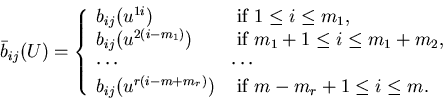
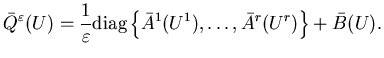 |
(5.54) |
|
|
(5.55) |
We next define the limiting problem. For ![]() ,
define
,
define
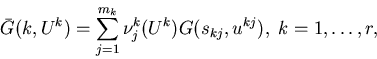
We define the limiting problem with the long-run average cost.
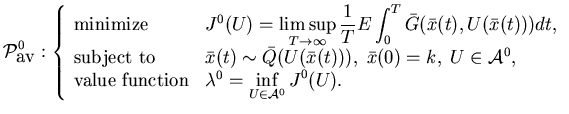 |
(5.56) |
|
|
(5.57) |
Theorem 5.12 (i) There
exists a pair![]() that
satisfies the DP equation (5.57).
that
satisfies the DP equation (5.57).
(ii) The DP equation (5.57)
has
a unique solution in the sense that for any other solution![]() to
(5.57),
to
(5.57),![]() and
and![]() ,
for
some constant K.
,
for
some constant K.
(iii) Let![]() denote
a minimizer of the right-hand side of (5.57).
Then
denote
a minimizer of the right-hand side of (5.57).
Then![]() is
optimal, i.e.,
is
optimal, i.e.,![]() .
.
Remark 5.5 Note that the number
of the DP equations for ![]() is equal to
is equal to![]() ,
while the number of that for
,
while the number of that for ![]() is only r. Since for each
is only r. Since for each ![]() ,
,![]() ,
it follows that
,
it follows that ![]() .
The difference between
m and r could be very large for either
large r or a large
mk for some k. Since
the computational effort involved in solving the DP equations depends largely
on the number of the equations to be solved (cf. Hillier
and Lieberman (1989)), the effort in solving the DP equations for
.
The difference between
m and r could be very large for either
large r or a large
mk for some k. Since
the computational effort involved in solving the DP equations depends largely
on the number of the equations to be solved (cf. Hillier
and Lieberman (1989)), the effort in solving the DP equations for ![]() is substantially less than that of solving
is substantially less than that of solving ![]() for m-r large.
for m-r large.
We construct a control ![]() as follows:
as follows:
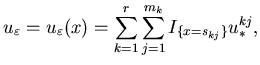 |
(5.58) |
Theorem 5.13 Let![]() denote
an optimal control for
denote
an optimal control for![]() and
let
and
let![]() be
the corresponding control constructed as in (5.58).
Then,
be
the corresponding control constructed as in (5.58).
Then,![]() is
asymptotically optimal and with error bound
is
asymptotically optimal and with error bound![]() ,
i.e.,
,
i.e.,
Remark 5.6 Filar,
Haurie, Moresino, and Vial (1999) introduce diffusions in these models;
see Remark 4.5. In their model, all jumps
are associated with a slow process, while the continuous part including
the diffusions is associated with a small parameter ![]() (see Remark 4.5) representing a fast process.
As
(see Remark 4.5) representing a fast process.
As ![]() tends to zero, the problem is shown to reduce to a structured linear program.
Its optimal solution can then be used as an approximation to the optimal
solution of the original system associated with a small
tends to zero, the problem is shown to reduce to a structured linear program.
Its optimal solution can then be used as an approximation to the optimal
solution of the original system associated with a small ![]() .
.