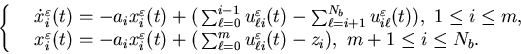
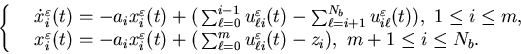
| = | |||
| = | (5.37) |
Our problem is to find an admissible control![]() that minimizes the cost function
that minimizes the cost function
![$\displaystyle J^{\epsilon}({\mbox{\boldmath$x$ }}, {\mbox{\boldmath$m$ }})=\lim......oldmath$x$ }}^{\varepsilon}(t))+c({\mbox{\boldmath$u$ }}^{\varepsilon}(t))]dt,$](img980.gif) |
(5.38) |
In place of Assumptions 3.4, 3.5
and 3.6 in Section 3.3
on the cost function ![]() and
and ![]() and the machine capacity process
and the machine capacity process![]() ,
we impose the following assumptions on the random process
,
we impose the following assumptions on the random process![]() throughout this section.
throughout this section.
Assumption 5.5 Let ![]() ,
and
,
and ![]() for
for![]() ,
that is, pn is the average capacity of the machine n,
and n(i,j) is the number of the machine located on
the arc (i,j). Furthermore, we assume that there exist
,
that is, pn is the average capacity of the machine n,
and n(i,j) is the number of the machine located on
the arc (i,j). Furthermore, we assume that there exist![]() such that
such that
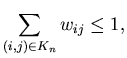 |
(5.39) | ||
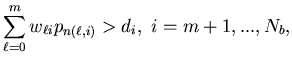 |
(5.40) |
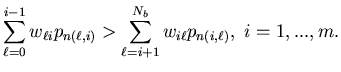 |
(5.41) |
|
|
(5.42) |
In the case of the long-run average cost criterion used here, we know,
by Theorem 2.4 in Presman, Sethi, and Zhang
(1999b), that under Assumption 5.5,![]() is independent of the initial condition
is independent of the initial condition ![]() .
Thus we will use
.
Thus we will use ![]() instead of
instead of ![]() .
We use
.
We use ![]() to denote our control problem, i.e.,
to denote our control problem, i.e.,
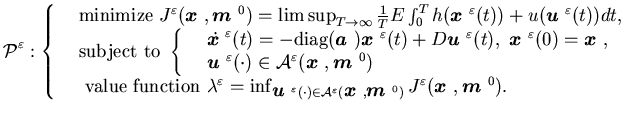 |
(5.43) |
As in Section 5.1, the positive attrition
rate![]() implies a uniform bound for
implies a uniform bound for ![]() .
.
Next we examine elementary properties of the potential function and
obtain the limiting control problem as ![]() .
.
The Hamilton-Jacobi-Bellman equation in the directional derivative sense
with the average-cost optimal control problem in ![]() ,
as shown in Sethi, Zhang, and Zhang (1999b),
takes the form
,
as shown in Sethi, Zhang, and Zhang (1999b),
takes the form
| = | 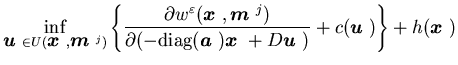 |
||
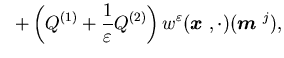 |
(5.44) |
First we can get the boundedness of ![]() .
.
Theorem 5.9 The minimum
average expected cost ![]() of
of ![]() is
bounded in
is
bounded in![]() ,
i.e.,
there exists a constant M1>0
such that
,
i.e.,
there exists a constant M1>0
such that
For the proof, see Sethi, Zhang, and Zhang (1999b).
Now we derive the limiting control problem as ![]() .
As in Sethi and Zhou (1994), we give the
following definition.
.
As in Sethi and Zhou (1994), we give the
following definition.
Definition 5.6 For ![]() ,
let
,
let ![]() denote the set of the following measurable controls
denote the set of the following measurable controls
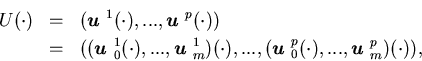
such that ![]() for all
for all ![]() ,
j=1,...,p,
and n=1,...,nc, and the corresponding solutions
,
j=1,...,p,
and n=1,...,nc, and the corresponding solutions![]() of the following system
of the following system
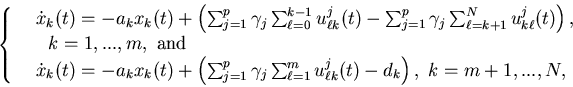
![\begin{displaymath}J( U(\cdot))=\limsup_{T \rightarrow \infty} \frac {1} {T} \......(s))+\sum_{j=0} ^p\gamma_j c({\mbox{\boldmath$u$ }}^j(s))]ds.\end{displaymath}](img922.gif)
We use ![]() to denote the above problem, and will regard this as our limiting problem.
Then we define the limiting control problem
to denote the above problem, and will regard this as our limiting problem.
Then we define the limiting control problem ![]() as follows:
as follows:
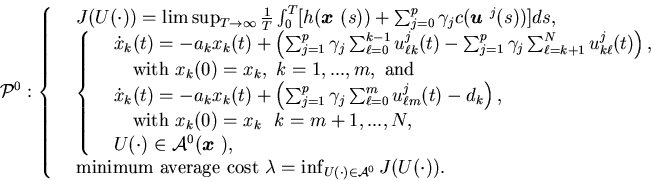
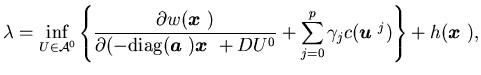 |
(5.45) |
where ![]() is a potential function for
is a potential function for ![]() and
and![]() is the directional derivative of
is the directional derivative of![]() along the direction
along the direction![]() with
with![]() .
From Presman, Sethi, and Zhang (1999b),
we know that there exist
.
From Presman, Sethi, and Zhang (1999b),
we know that there exist ![]() and
and ![]() such that (5.45) holds. Moreover,
such that (5.45) holds. Moreover, ![]() is the limit of
is the limit of ![]() as
as ![]() .
.
Now we are ready to discuss the convergence of the minimum average expected
cost ![]() as
as ![]() goes to zero, and establish the corresponding convergence rate. First we
give two lemmas which are used in proving the convergence.
goes to zero, and establish the corresponding convergence rate. First we
give two lemmas which are used in proving the convergence.
Lemma 5.7 For ![]() and
any sufficiently small
and
any sufficiently small![]() ,
there
exist
,
there
exist![]() ,
,![]() ,
and
,
and
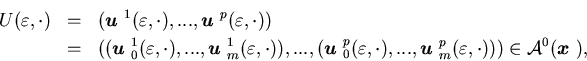
 |
(5.46) |
![$\displaystyle \lambda +\hat C_{54} \varepsilon^{\delta}>\limsup_{T \rightarrow......))+\sum_{j=1}^p\gamma_j c({\mbox{\boldmath$u$ }}^j(\varepsilon, t))\right]dt,$](img1004.gif) |
(5.47) |
where ![]() is the trajectory under
is the trajectory under ![]()
Lemma 5.8 For ![]() ,
there exist
,
there exist![]() ,
and
,
and![]() ,
and
,
and
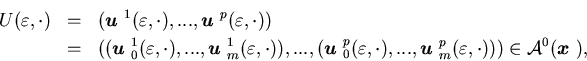
|
|
(5.48) |
![$\displaystyle \lambda + \hat C_{55} \varepsilon^{\delta}>\limsup_{T \rightarro......t))+\sum_{i=1}^p\gamma_i c({\mbox{\boldmath$u$ }}^i(\varepsilon, t))\right]dt,$](img1007.gif) |
(5.49) |
where ![]() is the state trajectory under the control
is the state trajectory under the control ![]() .For
the proof of Lemmas 5.7 and 5.8,
see Sethi, Zhang, and Zhang (1999b).
.For
the proof of Lemmas 5.7 and 5.8,
see Sethi, Zhang, and Zhang (1999b).
Using these two lemmas, Sethi, Zhang, and Zhang (1999b) derive the following theorem.
Theorem 5.10 For any ![]() there exists a constant
there exists a constant ![]() such that for all sufficiently small
such that for all sufficiently small![]()
|
|
(5.50) |
This implies in particular that ![]()
Remark 5.4 The theorem says
that the problem![]() is indeed a limiting problem in the sense that the
is indeed a limiting problem in the sense that the![]() of
of ![]() converges to
converges to ![]() of
of ![]() .
Moreover, it gives the corresponding convergence rate.
.
Moreover, it gives the corresponding convergence rate.